Φιλοσοφία και ρύθμιση αντιστάθμισης

Γενικά

Ως γνωστόν η αντιστάθμιση αντισταθμίζει με την παρουσία της στο σύστημα την δεδομένη ισχύ αυτού επεμβαίνοντας σε μία σημαντική παράμετρο για την ισχύ του συστήματος που είναι η θερμοκρασία του νερού προς τα θερμαντικά σώματα ή τα ενδοδαπέδια κυκλώματα. Η αντιστάθμιση κρίνεται αναγκαία σε συνθήκες όπου δεν επικρατεί η ελάχιστη ακραία εξωτερική θερμοκρασία. Επειδή οι συνήθεις εξωτερικές θερμοκρασίες στην πλειοψηφία των χειμερινών ωρών λειτουργίας των συστημάτων θέρμανσης είναι κατά μεγάλη πλειοψηφία μακριά από την ακραία συνθήκη βάσει της οποίας μελετήθηκε το σύστημα, η αντιστάθμιση επεμβαίνει με σκοπό να χαμηλώσει την ισχύ του συστήματος και να την προσομοιώσει με εκείνη που θα χρειαζόταν αν η μελέτη του συστήματος γινόταν με γνώμονα την επικρατούσα εξωτερική θερμοκρασία και όχι εκείνη που εξέλαβε ως ακραία ο μελετητής. Η παρέμβαση αυτή όπως είπαμε γίνεται μέσω της θερμοκρασίας νερού με δύο τρόπους:

·    Διά της μεθόδου ανάμιξης μέσω μιας τρίοδης ή τετράοδης βαλβίδας

·    Διά της μεθόδου ελάττωσης της θερμοκρασίας του νερού του λέβητα από σύστημα αντιστάθμισης που περιέχει ο ίδιος ο λέβητας όπως γίνεται με τους επίτοιχους αερίου ή τους λέβητες πετρελαίου με ειδικό πίνακα οργάνων.

Κάθε σύστημα όμως έχει τις δικές του παραμέτρους όσον αφορά την λογική της μείωσης της ισχύος την οποία θα δούμε παρακάτω. Άρα και κάθε σύστημα πρέπει να ρυθμίζεται βάσει της δικής του ταυτότητας και όχι να αφήνεται στην τύχη του. Την δουλειά αυτή μόνο ο μηχανολόγος που μελέτησε το σύστημα μπορεί να την κάνει. Ειδάλλως χρειάζεται εξειδικευμένο άτομο και πολύ έμπειρο όχι μόνο με τα ηλεκτρονικά αλλά να γνωρίζει και τις λεπτομέρειες της θέρμανσης όπως τις γνωρίζει ο μηχανολόγος. Θα έλεγα ότι τέτοιοι έμπειροι και εξειδικευμένοι στα συστήματα αντιστάθμισης πρέπει κατά πρώτον να είναι μηχανολόγοι και όχι ο εξειδικευμένος τεχνικός-ηλεκτρονικός της άλφα ή της δείνα εταιρείας.

 

Στα ενδότερα της αντιστάθμισης

Υπολογισμός συντελεστή φορτίου του συστήματος μ για
μία πιθανή εξωτερική θερμοκρασία t

Έστω ότι ένα σύστημα έχει μελετηθεί για εξωτερική ακραία συνθήκη 0° και για εσωτερική θερμοκρασία χώρων 20°, να αποδίδει ισχύ Ν­_R ίση με το 100% της ισχύος του που σημαίνει ότι ο συντελεστής φορτίου του  ισούται με τη μονάδα. Αν η εξωτερική θερμοκρασία είναι στους 20° τότε δεχόμαστε ότι το σύστημα θα παρέχει ισχύ Ν_n ίση με το 0% της ισχύος του. Επειδή η μεταβολή είναι γραμμική τότε αν η εξωτερική θερμοκρασία είναι στους 10° το σύστημα θα παρέχει το 50% της ισχύος του (συντελεστής φορτίου ίσος με 0,5) και τελικά στη γενική του μορφή ο βαθμός αυτός μ προέρχεται από την εξίσωση ευθείας με την γενική μορφή:

   (1)      όπου:

t   à Τυχαία εξωτερική θερμοκρασία για την οποία ισχύει ο συντελεστής φορτίου μ_t

t_h à Μέση θερμοκρασία χώρων βάσει της οποίας υπολογίσθηκαν τα θερμικά φορτία του κτηρίου.

t_c  à Ακραία εξωτερική θερμοκρασία βάσει της οποίας υπολογίσθηκαν τα θερμικά φορτία του κτηρίου.

 

Υπολογισμός θερμοκρασίας εισόδου μειωμένου συστήματος

Είπαμε παραπάνω ότι η αντιστάθμιση παρεμβαίνει στην μείωση της ισχύος του συστήματος όταν αντιληφθεί ότι η εξωτερική θερμοκρασία είναι μεγαλύτερη της ακραίας κατά την οποία σχεδιάσθηκε το σύστημα. Επίσης είπαμε ότι αν θεωρήσουμε την ακραία ισχύ του συστήματος ως N_R­­ και την νέα ισχύ που θα επιλέξει η αντιστάθμιση βάσει της εξωτερικής θερμοκρασίας t, ως N_n τότε ισχύει η σχέση: . Από την θεωρία όμως της μεταφοράς θερμότητας στα θερμαντικά σώματα γνωρίζουμε επίσης ότι:

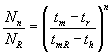, συνεπώς και  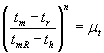όπου:

t_m à Νέα μέση θερμοκρασία εισόδου/εξόδου[1] του νερού προς και από το σύστημα

t_r à Επιθυμητή θερμοκρασία χώρων κατά την μείωση. Συνήθως δεν αλλάζει και είναι ίση με αυτήν του αρχικού σχεδιασμού t_h

t_mR à Μέση θερμοκρασία νερού εισόδου/εξόδου προς και από το σύστημα κατά το 100% της ισχύος του.

t_h à Όπως είπαμε παραπάνω η μέση θερμοκρασία των χώρων που έλαβε υπ’ όψη του ο μελετητής.

n à Ο γνωστός συντελεστής μεταφοράς θερμότητας από τα θερμαντικά σώματα φυσικής κυκλοφορίας προς τον αέρα του χώρου και που ισούται με n=1,33.

μ_t à Συντελεστής φορτίου για την συγκεκριμένη εξωτερική θερμοκρασία.

Ξεκινώντας λοιπόν από την παραπάνω σχέση: 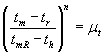 και μετά από λίγες μαθηματικές πράξεις καταλήγουμε στην παρακάτω σχέση:

   (2)

όπου την λύσαμε ως προς t_in, ακριβώς το μέγεθος που μας ενδιαφέρει. Η παράμετρος Cf ισούται με  όπου Δt_n à η νέα διαφορά θερμοκρασίας εισόδου/εξόδου προς και από το σύστημα που θα προκύψει από την μείωση που θα κάνει η αντιστάθμιση. Υπάρχουν δύο λογικές στα σημερινά συστήματα όσον αφορά τις ροές και τα Δt που προκύπτουν κατά την μείωση της ισχύος ενός συστήματος:

·    Το σύστημα διατηρεί τις ροές αμετάβλητες και μεταβάλλεται το νέο Δt. Αυτή είναι και η πλειοψηφία των συστημάτων μεταβλητής ισχύος λόγω αντιστάθμισης. Οπότε στην περίπτωση αυτή έχουμε:                      (3_α)

·    Το σύστημα λειτουργεί με σταθερά Δt και μεταβάλλει τις ροές μέσω ενός ηλεκτρονικού κυκλοφορητή. Το τελευταίο είναι μία επιλογή που συναντά κανείς στα επίτοιχα λεβητάκια φυσικού αερίου. Στην περίπτωση αυτή ισχύει:                  (3_β)

Επιλογή της κατάλληλης, για το κτήριο, καμπύλης Κ

Οι γνωστές καμπύλες Κ που συναντάμε στα ηλεκτρονικά μέρη των αντισταθμίσεων του εμπορίου, στον άξονα των τετμημένων έχουν την πιθανή εξωτερική θερμοκρασία του περιβάλλοντος κατά φθίνουσα σειρά ενώ στον άξονα των τεταγμένων έχουν την κατάλληλη θερμοκρασία νερού ως εισόδου στα θερμαντικά σώματα κατά αύξουσα σειρά την οποία και θα πετύχει η αντιστάθμιση. Εδώ να πούμε ότι κάθε κτήριο, και από πλευράς τοποθεσίας αλλά και από πλευράς συστήματος, βάσει των παραπάνω, έχει την δική του καμπύλη Κ την οποία πρέπει να επιλέγει ο χρήστης αφού πρώτα την υπολογίσει[2]. Και εδώ εισέρχεται το engineering point of view του φαινομένου. Αντιλαμβανόμαστε ότι οι παραπάνω συναρτήσεις μέσα στα πεδία των τιμών που ενδιαφερόμαστε, δίνουν καμπύλες που πρακτικά είναι ευθείες γραμμές! Διαφέρουν μόνο στο πρώτο δεκαδικό ψηφίο και συνήθως σε τιμές που είναι κάτω του μισού βαθμού. Εφόσον λοιπόν αντιμετωπίζουμε την καμπύλη σαν ευθεία γραμμή αρκεί να βρούμε δύο σημεία της ώστε να την ορίσουμε πλήρως. Ας δούμε ένα παράδειγμα:

 

 

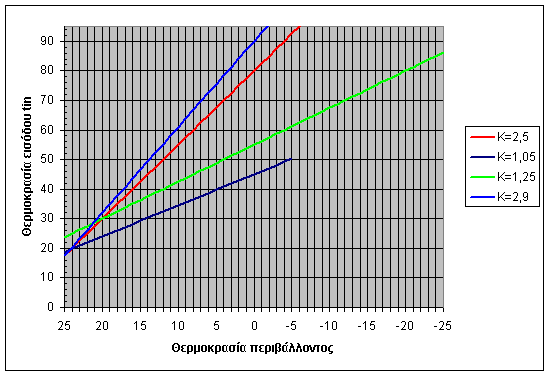
Το παραπάνω διάγραμμα αναπαριστά τέσσερις διαφορετικές καμπύλες που έχουν τιμές Κ οι οποίες αναφέρονται δεξιά στο διάγραμμα. Τα δεδομένα των τεσσάρων καμπυλών καταγράφονται στον παρακάτω πίνακα:

 

 

 

Οι παραπάνω ευθείες πρέπει να εισαχθούν στην πλακέτα της αντιστάθμισης η οποία δεν γνωρίζει τίποτα από αυτά που γράφτηκαν στις προηγούμενες σελίδες και δεν κάνει εκθετικούς και λογαριθμικούς υπολογισμούς. Το μόνο που θέλει η πλακέτα ώστε να υπολογίσει την νέα ζητούμενη θερμοκρασία εισόδου στο σύστημα -t_in- είναι δύο πληροφορίες:

·    Τον συντελεστή κατεύθυνσης της ευθείας ο οποίος είναι ο αντίθετος αριθμός του συντελεστή Κ. Δίνοντας ο χρήστης τον συντελεστή Κ τότε η πλακέτα γνωρίζει τον συντελεστή κατεύθυνσης της ευθείας ή άλλως την εφαπτομένη της οξείας γωνίας με τον άξονα των εξωτερικών θερμοκρασιών.

·    Δεν φτάνει όμως μόνο η γωνία για να γνωρίζει η πλακέτα την συγκεκριμένη ευθεία. Χρειάζεται ένα ακόμα σημείο το οποίο καλείται: «reference point[3]» («αρχικό σημείο» σε αρκετά ελληνικά φυλλάδια). Αυτό το σημείο υπολογίζεται από τον χρήστη[4] και δηλώνεται στη πλακέτα μέσω του ηλεκτρονικού χειριστηρίου της.

Τώρα πλέον η πλακέτα γνωρίζουσα πλήρως την συγκεκριμένη ευθεία που ταιριάζει στο συγκεκριμένο κτήριο καθώς και την εκάστοτε εξωτερική θερμοκρασία μέσω του εξωτερικού αισθητηρίου, μπορεί να υπολογίζει την εκάστοτε θερμοκρασία νερού που πρέπει να στέλνει προς το σύστημα θέρμανσης είτε σε θερμαντικά σώματα, είτε σε ενδοδαπέδια κυκλώματα.

Περίπτωση υπερδιαστασιολογημένου συστήματος:

Στη πληθώρα των εγκαταστάσεων υπάρχει ως γνωστόν η κακή συνήθεια του παρελθόντος (ακόμη και του παρόντος) να υπερδιαστασιολογούνται τα θερμαντικά σώματα καθώς και ο λέβητας όπως και ο κυκλοφορητής. Για τα δύο τελευταία η αντιστάθμιση δεν μπορεί να προσφέρει κάποια βοήθεια. Μπορεί όμως να μετριάσει την υπερδιαστασιολόγηση των θερμαντικών σωμάτων λαμβάνοντάς την υπ’ όψιν στον υπολογισμό της κατάλληλης καμπύλης του συστήματος. Αν λοιπόν έχουμε μία υπερδιαστασιολόγηση στα θερμαντικά σώματα α_h% τότε η παραπάνω εξίσωση (1) που υπολογίζει τον συντελεστή φορτίου για την πιθανή εξωτερική θερμοκρασία t_o μεταβάλλεται ως εξής:

   (4)       όπου:

t_o à Πιθανή εξωτερική θερμοκρασία για την οποία ισχύει ο συντελεστής φορτίου t_o

t_h à Μέση θερμοκρασία χώρων βάσει της οποίας υπολογίσθηκαν τα θερμικά φορτία του κτηρίου.

t_c  à Ακραία εξωτερική θερμοκρασία βάσει της οποίας υπολογίσθηκαν τα θερμικά φορτία του κτηρίου.

α_h à % προσαύξηση είτε των θερμαντικών σωμάτων είτε των θερμικών φορτίων που υπολογίσθηκαν για ασφάλεια βάσει των παλιών συνηθειών των καιρών που έλαβε χώρα η μελέτη του κτηρίου.

 

Πρέπει δε να υπολογίζεται εκ νέου και για τις δύο εξωτερικές θερμοκρασίες που λαμβάνει υπ’ όψιν του ο υπολογισμός της καμπύλης Κ. Από το σημείο αυτό και στη συνέχεια, ο τρόπος υπολογισμού της καμπύλης δεν αλλάζει και παραμένει ο αυτός.

 

 

 

Παράδειγμα εύρεσης μιας καμπύλης αντιστάθμισης για δεδομένη πολυκατοικία

Ας πάμε να υπολογίσουμε την καμπύλη μιας πολυκατοικίας με θερμαντικά σώματα τύπου πάνελς που έχει τα παρακάτω δεδομένα μελέτης:

 

Το σύστημα είναι σταθερής ροής κατά τον χρόνο που μειώνεται η ισχύς του και λειτουργεί όπως φαίνεται στο 100% της ισχύος του με ένα Δt=15°. Τα παραπάνω αρκούν για να υπολογίσουμε την καμπύλη της αντιστάθμισης.

1.    Εν πρώτοις πρέπει να υπολογισθεί ο συντελεστής φορτίου μ_t για μία οιαδήποτε εξωτερική θερμοκρασία t. Εδώ επιλέγω μία εξωτερική πιθανή θερμοκρασία της αρεσκείας μου την οποία και κρατώ[5]. Έστω ότι t = 10°. Από την σχέση (1) έχω:

2.    Αμέσως μετά υπολογίζω για την συγκεκριμένη εξωτερική θερμοκρασία, την απαιτούμενη για το σύστημα θερμοκρασία εισόδου στο σύστημα των θερμαντικών σωμάτων ή των ενδοδαπέδιων κυκλωμάτων. Από τις σχέσεις (2) & (3_α) έχω:

3.    Τώρα έχοντας στην διάθεσή μου τις συντεταγμένες δύο σημείων της ευθείας (της καμπύλης αντιστάθμισης), είμαι σε θέση να βρω τον συντελεστή Κ αλλά και το reference point ήτοι τις δύο παραμέτρους που ζητά η αντιστάθμιση. Τα δύο πλέον γνωστά μου σημεία της ευθείας είναι τα:

 

3.1.       Ο συντελεστής κατεύθυνσης της ευθείας είναι ως γνωστόν:

 άρα και ο αντίθετος αυτού Κ=2,5

3.2.       Το reference point y₃ (για x₃=20°), βρίσκεται από τις γνωστές σχέσεις που ισχύουν μεταξύ των συντεταγμένων μιας ευθείας γραμμής και που είναι:

ή μέσω του άλλου σημείου που ξέρουμε (x₁,y₁):

 

4.    Αν είχα στα σώματα μία υπερδιαστασιολόγηση της τάξης του 25% τότε το παραπάνω πινακάκι, σύμφωνα με τα παραπάνω, μεταβάλλεται ως ακολούθως:

και συνεπώς ο νέος Κ της καμπύλης ισούται: Κ=2,1 το δε reference point αυτής θα είναι το σημείο: y₃=28,5°. Βλέπουμε ότι είναι μία άλλη καμπύλη σε σχέση με την προηγούμενη όπου η μεν πρώτη για 5° εξωτερική θερμοκρασία δίνει 67,5° θερμοκρασία νερού στα σώματα η δε δεύτερη δίνει 60°. Αυτός είναι ο καταλληλότερος τρόπος για να αντιμετωπισθεί εκτός των άλλων και μία τυχόν υπερδιαστασιολόγηση που έγινε στο σύστημα κατά την ώρα της κατασκευής του.

 

 

Τώρα πλέον και βάσει των παραπάνω έχουμε στην διάθεσή μας όλα τα στοιχεία ώστε να ρυθμίσουμε αφενός οιαδήποτε αντιστάθμιση και αφετέρου να την ελέγξουμε βάσει των πραγματικών συνθηκών που θα προκύψουν κατά τη γενική δοκιμή στο έργο.

Να προσθέσω δε ότι η παραπάνω 4^η παράγραφος που αφορά την υπερδιαστασιολόγηση των θερμαντικών σωμάτων ή των θερμικών φορτίων των διαμερισμάτων, αν υπολογισθεί σωστά ο αντίστοιχος Κ καθώς και η το σημείο αναφοράς της καμπύλης τότε θα προκύψει οικονομικότερη λειτουργία για όλο το κτήριο και σε επίπεδα μάλιστα αρκετά ικανοποιητικά για τους ενοίκους του.

 

 

         Φεβρουάριος του 2011

         Γιώργος Βαρβαγιάννης

         Μηχανολόγος Μηχανικός