Υδραυλικά δίκτυα

Σχετικά με το άρθρο αυτό
Το άρθρο αυτό δημοσιεύθηκε εν έτει 1995 σε δύο συνέχειες στα τεύχη 280/95 & 281/96 του δελτίου του ΠΣΔΜΗ. Συγγραφείς του άρθρου αυτού είναι οι μηχανικοί Βαρβαγιάννης Γιώργος και Σανδαλίδης Χρήστος

Εφαρμοσμένα υδραυλικά δίκτυα μεταφοράς θερμικής ενέργειας

Εισαγωγή

Με την ολοκλήρωση του θερμικού μέρους μιας μελέτης ψύξης-θέρμανσης ( ή απλής θέρμανσης) ο μελετητής μηχανικός πρέπει πλέον να σχεδιάσει ένα δίκτυο νερού το οποίο θα επαληθεύει πλήρως (ή έστω με πολύ μικρές αποκλίσεις) στην πράξη, τις παροχές του νερού τις οποίες υπολόγισε στο θερμικό μέρος της μελέτης του. Οι απαιτήσεις των καιρών και η συνεχής έρευνα επάνω στα συστήματα αυτά, έδωσαν διάφορες τεχνικές αλλά και υλικά για την επίτευξη του σκοπού αυτού. Ουσιαστικά τρία είναι τα συστήματα υδραυλικών δικτύων που απαντώνται στις κατασκευές. Είναι τα:

Το γνωστό κλασσικό δίκτυο που υπολογίζει την αντλία βάσει του απομακρυσμένου βρόγχου.

Δίκτυο σε σύστημα Reverse return, το γνωστό αντεπίστροφο σύστημα.

Δίκτυο με εξισορρόπηση δευτερευόντων κλάδων που δύναται να είναι σε σχεδιασμό είτε κλασσικού είτε αντεπίστροφου συστήματος.

Παρακάτω κάνουμε μία γρήγορη αναφορά στα 3 παραπάνω είδη υδραυλικής σύνδεσης και κατόπιν εξετάζουμε και τα τρία συστήματα αυτά σε ένα αρκετά κατατοπιστικό και πρακτικό παράδειγμα.

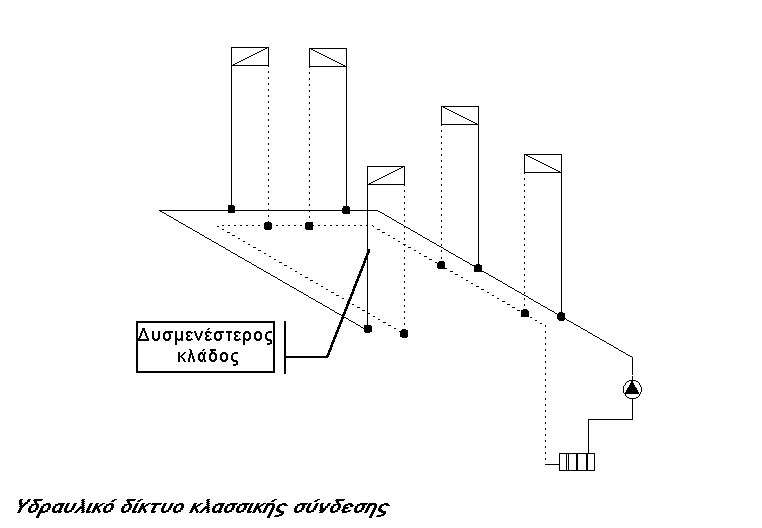
1. Κλασσικό δίκτυο

Η υδραυλική ανάλυση και ο υπολογισμός της αντλίας του δικτύου αυτού γίνεται βάσει του (κατά την γνώμη του μελετητή) δυσμενέστερου κλάδου. Υπολογίζουμε τις υδραυλικές αντιστάσεις του και στην συνέχεια μέσω των πρωτευόντων κλάδων (κύριο δίκτυο) όπου αναλύονται και αυτοί, φθάνουμε στην αντλία όπου και την επιλέγουμε. Υδραυλική ανάλυση δεν γίνεται σε κανέναν από τους δευτερεύοντες κλάδους που μεσολαβούν μεταξύ του απομακρυσμένου κλάδου και της αντλίας, παρά τους θεωρούμε (αυθαιρέτως) ότι δέχονται τις θεωρητικές παροχές νερού που θα θέλαμε να περνούν μέσα από αυτούς, τις οποίες αθροίζουμε μέχρις ότου φθάσουμε στην αντλία την οποία και επιλέγουμε βάσει του συνολικού αθροίσματος των παροχών αυτών. Στην πράξη βέβαια όταν λειτουργήσει η αντλία, θα στείλει το νερό με τελείως διαφορετική κατανομή στους κλάδους από εκείνη που αναφέρουν τα αναλυτικά φύλλα υδραυλικών υπολογισμών όπως θα δούμε και στο παράδειγμα. Οι επιπτώσεις βέβαια από αυτήν την «απειθαρχία» του δικτύου δεν είναι καθόλου ευκαταφρόνητες όπως έχουμε γράψει σε προηγούμενα άρθρα μας αλλά και αναφέρουμε παρακάτω στα γενικά σχόλια του παραδείγματος.

Τελικά είναι δίκτυο υδραυλικής ανάλυσης με τις μεθόδους του 1970 και οι μελετητές εκείνοι που είχαν άμεση επαφή με την πράξη, πρότειναν στους εργολάβους μια εμπειρική διόρθωση «γνωστή σαν μέθοδο στραγγαλισμού» με μερικό κλείσιμο των κεντρικών βανών (συρταρωτών την εποχή εκείνη), είτε του κυκλοφορητή είτε των κεντρικών συλλεκτών του λέβητα. Σπανιότερα ακόμη ορισμένοι εργολάβοι προέβαιναν (εμπειρικά πάντα) και σε κάποια ρύθμιση των διακοπτών των θερμαντικών σωμάτων (αναφέρομαι στα δισωλήνια συστήματα) την οποία και σταθεροποιούσαν μέσω των μεθόδων προρύθμισης των συγκεκριμένων διακοπτών. Κατ’ αυτόν τον τρόπο έκαναν μία εξισορρόπηση στο δίκτυο έτσι ώστε ελαχιστοποιούταν η αστοχία του δικτύου.

2. Δίκτυο Reverse return ή Αντεπίστροφο σύστημα

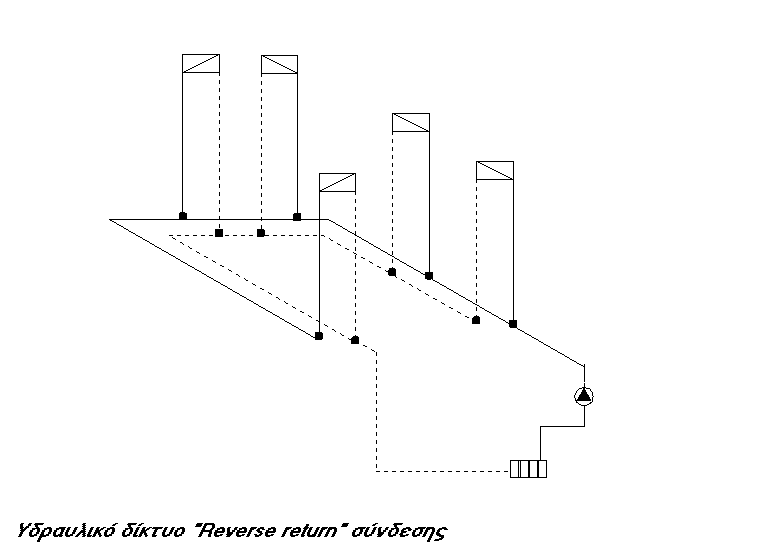
Ο βασικός λόγος πού γεννήθηκε σαν ιδέα ήταν τα μεγάλα σε μήκος οριζόντια δίκτυα και η ανυπαρξία ειδικών εξισορροπητικών βαλβίδων των δικτύων την εποχή εκείνη. Ονομάσθηκε αντεπίστροφο (reverse-return system) διότι ο σωλήνας επιστροφής δεν επιστρέφει από το σημείο που έρχεται ο σωλήνας εισαγωγής αλλά από την αντίστροφη κατεύθυνση. Η τάση του συστήματος αυτού είναι να αυτοεξισορροπηθεί μετασχηματίζοντας όλο το κύριο (οριζόντιο ή κατακόρυφο) δίκτυο έτσι, που να συμπεριφέρεται όσον αφορά τους κλάδους σαν ένας συλλέκτης εισαγωγής-επιστροφής. Επίσης η φύση του συστήματος αυτού είναι τέτοια ώστε να χαμηλώνει τις απαιτήσεις του μανομετρικού ύψους της αντλίας όπως θα δούμε παρακάτω στο παράδειγμα των τριών διαφορετικών συστημάτων δικτύων. Είναι δίκτυο περιμετρικού αλλά και βιομηχανικού (θα έλεγα μεγάλων εγκαταστάσεων) χαρακτήρα. Το αντεπίστροφο σύστημα λειτουργεί θαυμάσια από μόνο του χωρίς καμία εξισορρόπηση αλλά με δύο προϋποθέσεις, μία σημαντική και μία δευτερεύουσα. Τις διαχωρίζω κατ’ αυτό τον τρόπο διότι δεν έχει η κάθε μία χωριστά την ίδια βαρύτητα επίδρασης επάνω στο δίκτυο όπως θα δούμε παρακάτω στο παράδειγμα που ακολουθεί.

Βασική προϋπόθεση είναι ότι πρέπει οι δευτερεύοντες κλάδοι να είναι υδραυλικά ισοδύναμοι (διατομές, συντελεστές ζ κλπ) και ταυτόχρονα οι ροές που περνούν μέσα από αυτούς να είναι ίσες μεταξύ τους

Η δευτερεύουσα προϋπόθεση είναι ότι πρέπει οι διατομές του κυρίως δικτύου να είναι αρκετά μεγάλες, ούτως ώστε οι υδραυλικές αντιστάσεις τους να θεωρούνται πρακτικά αμελητέες. Δηλαδή η πτώση πίεσης ανά μέτρο μήκους του σωλήνα να μην υπερβαίνει τα 10 mm Υ.Σ. (αντιοικονομική απαίτηση!).

Στην περίπτωση που δεν ισχύει η βασική προϋπόθεση, τότε το αντεπίστροφο σύστημα όσον αφορά τον εξισορροπητικό του χαρακτήρα είναι μία ουτοπία! (Βλ. παράδειγμα παρακάτω). Η προϋπόθεση αυτή όμως συναντάται σε πολύ μεγάλες τυποποιημένες εγκαταστάσεις ή σε μικρά και μεγάλα ηλιακά συστήματα όπου τότε το σύστημα αυτό αποδεικνύεται χρησιμότατο.

3. Κλασσικό δίκτυο με εξισορροπημένους κλάδους

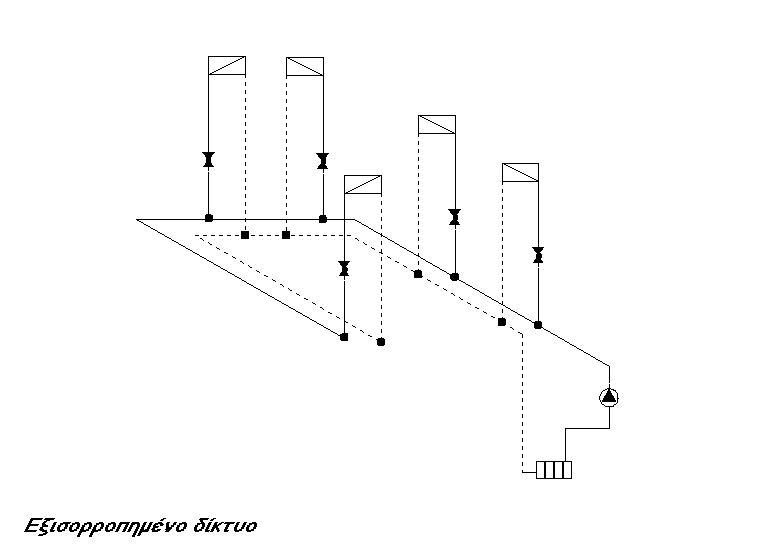
Ένα δίκτυο λέγεται εξισορροπημένο όταν έχουν προβλεφθεί από τον μελετητή ειδικές ρυθμιστικές αντιστάσεις στους δευτερεύοντες κλάδους. Οι αντιστάσεις αυτές (mm Υ.Σ ) δίνονται συνήθως με την μορφή των Kv (Βλ. επόμενη παράγραφο). Θα μπορούσαν βέβαια να δοθούν κατ’ ευθείαν σε mm Υ.Σ αλλά αυτό θα δυσκόλευε τον εργολάβο ο οποίος θα έπρεπε να ανατρέξει στις αντίστοιχες παροχές νερού των κλάδων, και να υπολογίσει μόνος του τις απαιτούμενες στροφές της εκάστοτε ρυθμιστικής βαλβίδας από τα νομογράμματά της. Με τον αριθμό Kv όμως, μπορεί να έχει τις στροφές κάθε βαλβίδας από ένα απλό πινακάκι του κατασκευαστή της, στην περίπτωση δε που οι μελετητές προδιαγράφουν συγκεκριμένης μάρκας υλικά, είναι πολύ εύκολο γι’ αυτούς κάτω από τον αριθμό Kv να καταχωρίσουν και τις αντίστοιχες στροφές των βαλβίδων αυτών επάνω στα κατασκευαστικά σχέδια.

Λίγα λόγια για τον αριθμό Kv ή Kvs

Οι υδραυλικές αντιστάσεις όπως γνωρίζουμε είναι συνάρτηση της ταχύτητας του νερού. Για τους σωλήνες η ταχύτητα (μέση ταχύτητα), ορίζεται πλήρως και είναι πρακτικά υπολογίσιμη ως το πηλίκο της παροχής του νερού δια της διατομής του σωλήνα. Για τα εξαρτήματα όμως πού δεν μπορεί να ορισθεί μία διατομή, δεν μπορούμε να γνωρίζουμε την ταχύτητα, συνεπώς και τις υδραυλικές αντιστάσεις. Στο παρελθόν στο σημείο αυτό υπήρχε θεωρητική ασάφεια διότι δεν γνωρίζαμε πως θα υπολογίσουμε τις υδραυλικές αντιστάσεις μέσα από κάποιο εξάρτημα, π.χ. μέσα από κάποια βαλβίδα. Συνηθιζόταν να παίρνουμε για τον υπολογισμό, την ταχύτητα του νερού μέσα στον αντίστοιχο σωλήνα σύνδεσης αυτού με την βαλβίδα, και μέσω του συντελεστή «ζ» να υπολογίζουμε κάποιες αντιστάσεις τις οποίες και δεχόμασταν de-facto. Πέραν όμως της παραπάνω θεωρητικής ασάφειας υπάρχει και το ακόλουθο πρακτικό παράδειγμα το οποίο συνηγορεί υπέρ της αμφισβήτησης του συντελεστή «ζ»:

Έστω ότι έχουμε τον ίδιον διακόπτη θερμαντικού σώματος τον οποίον συνδέουμε στο ίδιο θερμαντικό σώμα, με τρεις διαφορετικές διαμέτρους σωλήνων π.χ. 1/2’’ χαλύβδινη, Φ15 χάλκινη και Φ16 πλαστική, και έστω ότι από το θερμαντικό σώμα περνάμε μία παροχή νερού 300 Lit/h. Εξυπακούεται ότι οι υδραυλικές αντιστάσεις της βαλβίδας εφ’ όσον η παροχή του νερού και η βαλβίδα παραμένουν ως έχουν, είναι και στις 3 περιπτώσεις οι ίδιες. Βάσει του παραπάνω υπολογισμού όμως, έχω 3 διαφορετικές τιμές αντιστάσεων. Έστω ζ=6:

Είδος σωλήνα:	Χαλύβδινη 1/2’’	Χάλκινη Φ15x1	Πλαστική Φ16x2,5
Ταχύτητα (m/sec):	0,43	0,63	0,88
Υδραυλική αντίσταση (mm Υ.Σ):	57	122	237
Σφάλμα:	-53%	0%	+94%

Η αμφισβήτηση λοιπόν του συντελεστή «ζ» οδήγησε στον συντελεστή Kv ή Kvs ο οποίος έχει το πλεονέκτημα ότι συνδέει άμεσα την παροχή του νερού με τις υδραυλικές αντιστάσεις. Ορίζεται ως ακολούθως:

Ένα εξάρτημα έχει χαρακτηριστικό αριθμό 1 Kv όταν περνώντας μέσα από αυτό παροχή νερού G=1 m³/h, εμφανίζει πτώση πίεσης στα άκρα του ΔΡ=1 Bar. Ένα εξάρτημα έχει χαρακτηριστικό αριθμό 0,5 Kv όταν περνώντας μέσα από αυτό παροχή νερού G=0,5 m³/h, εμφανίζει πτώση πίεσης στα άκρα του ΔΡ=1 Bar. Δηλαδή ο Kv συνδέει την παροχή του νερού G πού περνά μέσα από το εξάρτημα με την πτώση πίεσης στα άκρα του ΔP και στην ουσία είναι ο αριθμός των κυβ.μ ανά ώρα που πρέπει να περάσουν για να εμφανισθεί ΔΡ=1 Bar. Δεχόμενοι από την Υδραυλική θεωρία ότι ο λόγος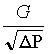 παραμένει σταθερός, μπορούμε να εμφανίσουμε την ακόλουθη εξίσωση:

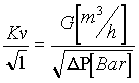
και η παραλλαγή αυτής:

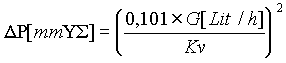
Στο Αγγλοσαξονικό σύστημα ο συντελεστής Kv απαντάται ως Cv. Ένα εξάρτημα έχει χαρακτηριστικό αριθμό 1 Cv όταν περνώντας μέσα από αυτό παροχή νερού 1 GPM εμφανίζεται στα άκρα του πτώση πίεσης ίση με 1 psi. Η σχέση που συνδέει το Kv και το Cv είναι:

Στο παραπάνω παράδειγμα αν η βαλβίδα έχει 1,7 Kv τότε εμφανίζει 320 mm Υ.Σ πτώση πίεσης στα άκρα της. Αυτή η τιμή έχει και πρακτική σημασία και όχι οι προηγούμενες οι οποίες είναι εξωπραγματικές. Όλοι οι κατασκευαστές οιονδήποτε τύπων βαλβίδων χρησιμοποιούν πλέον στα φύλλα προδιαγραφών των βαλβίδων αυτών τον αριθμό Kv, επομένως κρίνεται άκρως απαραίτητος για τους μελετητές υδραυλικών δικτύων που κατά την γνώμη μου πρέπει να εξοικειωθούν μαζί του.

Παράδειγμα και σύγκριση των 3 διαφορετικών συστημάτων δικτύου

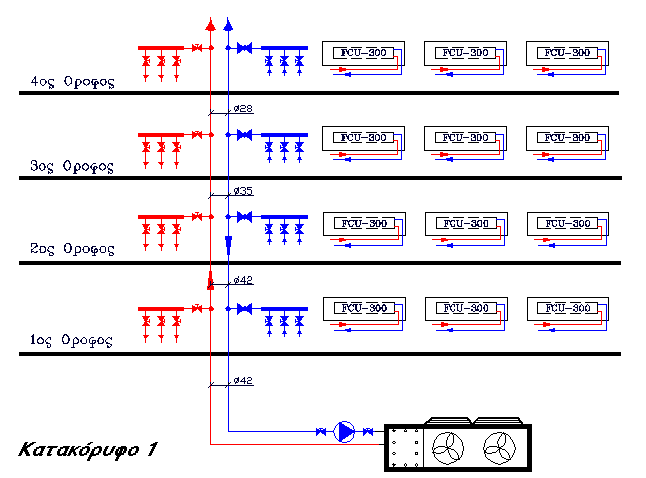
Επιλέξαμε για το παράδειγμα ένα τετραώροφο κτήριο όπου εφαρμόζουμε σύστημα ψύξης-θέρμανσης με fan-coils και μία κεντρική αντλία θερμότητας ως πηγή ψυκτικής-θερμικής ενέργειας των fan-coils αυτών. Το κτήριο αυτό είναι ένα συνηθισμένο κτήριο που απαντάται κατά κόρον τόσο στην Αθήνα όσο και στην επαρχία, και που στεγάζει κατοικίες ή γραφεία. Η διάταξη του δικτύου όπως άλλωστε φαίνεται και στο σχηματικό κατακόρυφο είναι:

Κύριο δίκτυο: Μία κεντρική στήλη που διαπερνά τους ορόφους. Τα υδραυλικά δεδομένα των κεντρικών στηλών από σημείο σε σημείο είναι: απόσταση 3 m, συντελεστής ζ=6, και οι διατομές φαίνονται στα σχήματα.

Δευτερεύον δίκτυο ή κλάδοι: Συλλέκτες ανά όροφο και τροφοδοσία των fan-coils με ενδοδαπέδια χαλκοσωλήνα.

Εξ’ αιτίας του αντεπίστροφου συστήματος επιλέξαμε να εξετασθεί το κτήριο ως οι ανάγκες του να επιβάλλουν δίκτυο:

Με ισοδυναμία δευτερευόντων κλάδων ανά όροφο και με τα δεδομένα του πίνακα Α.

Πίνακας Α

Επίπεδο	Απαιτούμενα Fan-coils	Απαιτούμενη ροή νερού ανά όροφο Lit/h	Υδραυλικές αντιστάσεις ανά όροφο mm Υ.Σ
Όροφος 1:	3 FCU-300	1350	2600
Όροφος 2:	3 FCU-300	1350	2600
Όροφος 3:	3 FCU-300	1350	2600
Όροφος 4:	3 FCU-300	1350	2600
		Σύνολο:5400

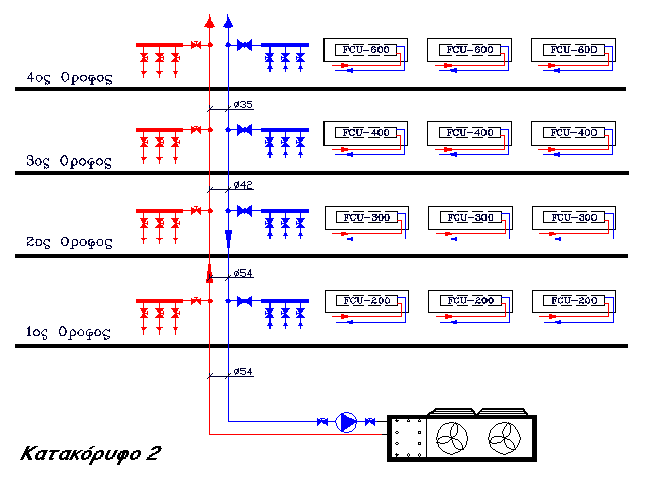
Με μη ισοδύναμους κλάδους και με τα δεδομένα του πίνακα Β, περίπτωση που είναι και η πλειοψηφία των εγκαταστάσεων αυτού του είδους.

Πίνακας Β

Επίπεδο	Απαιτούμενα Fan-coils	Απαιτούμενη ροή νερού ανά όροφο Lit/h	Υδραυλικές αντιστάσεις ανά όροφο mm Υ.Σ
Όροφος 1:	3 FCU-200	900	1100
Όροφος 2:	3 FCU-300	1350	2600
Όροφος 3:	3 FCU-400	1800	2800
Όροφος 4:	3 FCU-600	2700	4640
		Σύνολο:6750

Στο κλασσικό σύστημα όσο και στο αντεπίστροφο σύστημα, έχουμε κάνει την επιλογή της αντλίας βάσει της κλασσικής μεθόδου του απομακρυσμένου βρόγχου και δεχόμαστε ότι επιτυγχάνεται η συνολική απαιτούμενη παροχή νερού του συστήματος. Αυτό όμως που έχει ενδιαφέρον στην συνέχεια είναι το πως αυτή η συνολική παροχή νερού κατανέμεται στους ορόφους, εάν τελικώς έχουμε τις απαιτούμενες τιμές και εάν όχι τι αποκλίσεις υπάρχουν από αυτές. Για τον λόγο αυτόν σε κάθε περίπτωση που εξετάζεται ακολουθεί και ένας πίνακας με τα τελικά αποτελέσματα της ανάλυσης, δηλαδή ποια ποσότητα νερού περνά μέσα από κάθε κλάδο, υπερβάσεις-διαφορές σε σχέση με την ζητούμενη ποσότητα, καθώς και με ποια διαφορική πίεση εργάζεται το όλο σύστημα. Τέλος σε κάθε πίνακα προσθέτουμε μία στήλη ακόμη (την πέμπτη στήλη) όπου έχουμε πλέον μία εικόνα της διαφοράς που προκύπτει (άνοιγμα της ψαλίδας) μεταξύ δύο καταναλωτών, του ενδιαφερόμενου ορόφου και του πλέον ευνοημένου από το σύστημα όπως τελικώς λειτούργησε στην πράξη, όπως και του ενδιαφερόμενου ορόφου και του πλέον αδικημένου επίσης. Οι διαφορές αυτές των παροχών νερού μεταφράζονται (όπως αναφέρουμε στο τελικό σχόλιο του άρθρου) σε διαφορές παροχών ενέργειας όπου αυτές με την σειρά τους μεταφράζονται σε χρηματικές διαφορές μεταξύ των ενοίκων.

Η επιλογή των fan-coils στο παράδειγμα είναι τυχαία. Θα μπορούσε το κτήριο του παραδείγματος να λειτουργεί μόνο σε θέρμανση με θερμαντικά σώματα φυσικής κυκλοφορίας και σε διάταξη «σώμα και κύκλωμα» όπως άλλωστε είναι συνδεδεμένα και τα fan-coils του παραδείγματος. Τα αποτελέσματα των πινάκων θα ήταν περίπου τα ίδια και το γενικό συμπέρασμα που σκοπεύει το εν λόγω παράδειγμα δεν θα διέφερε.

Αρρύθμιστο δίκτυο

Α. Ισοδύναμοι κλάδοι
Περίπτωση 1.1.1 Σχήμα 1

Πίνακας 1.1.1

Επίπεδο	Ζητούμενη παροχή νερού Lit/h	Επιτευχθείσα παροχή νερού Lit/h	Απόκλιση από το ζητούμενο	Διαφορά από μέγιστη/ελάχιστη απόκλιση
Όροφος 1:	1350	1480	9,6%	0% / 20,3%
Όροφος 2:	1350	1390	3,0%	-6,5% / 13,0%
Όροφος 3:	1350	1300	-3,7%	-13,8% / 5,7%
Όροφος 4:	1350	1230	-8,9%	-20,3% / 0%
ΣΥΝΟΛΑ:	5400	5400
Απαιτούμενη διαφορική πίεση δικτύου: 3790 mmΥΣ

Σχόλια:

Η τελευταία στήλη δείχνει πόσο απέχει ο πρώτος κλάδος από τον τελευταίο και πόσο «δίκαια» μεταξύ τους παίρνουν το μερτικό τους. Υπάρχει λοιπόν μία εξήγηση που οι χρήστες των συστημάτων αυτονομίας, πολλές φορές παραπονιούνται ότι δεν συμβαδίζει το αποτέλεσμα της θέρμανσης με τις δαπάνες τους.

Παρακάτω εξετάζουμε (Πίνακας 1.1.2) τι θα συμβεί όταν μετά τις «διαμαρτυρίες» του 4ου ορόφου τοποθετηθεί μία ισχυρότερη αντλία ή αυξηθούν οι στροφές της ήδη υπάρχουσας.

Περίπτωση 1.1.2 Σχήμα 1

«Δυνάμωμα του προηγούμενου συστήματος»!

Έστω ότι μεταπηδώντας σε υψηλότερη καμπύλη του κυκλοφορητή βρίσκω το κανονικό σημείο λειτουργίας στα 4790 mm Υ.Σ, δηλαδή αυξάνεται η διαφορική πίεση του δικτύου κατά 1 m Υ.Σ. Η παροχή του νερού που προκύπτει στο συγκεκριμένο δίκτυο είναι 6070 Lit/h. Τι ακριβώς θα γίνει με την νέα κατάσταση, το αναλύει ο παρακάτω πίνακας 1.1.2

Πίνακας 1.1.2

Επίπεδο	Ζητούμενη παροχή νερού Lit/h	Επιτευχθείσα παροχή νερού Lit/h	Απόκλιση από το ζητούμενο	Διαφορά από μέγιστη/ελάχιστη απόκλιση
Όροφος 1:	1350	1660	23,0%	0% / 20,3%
Όροφος 2:	1350	1570	16,3%	-5,7% / 13,8%
Όροφος 3:	1350	1460	8,1%	-13,8% / 5,7%
Όροφος 4:	1350	1380	2,2%	-20,3% / 0%
ΣΥΝΟΛΑ:	5400	6070
Απαιτούμενη διαφορική πίεση δικτύου: 4790 mmΥΣ

Σχόλια:

Υπήρξε κάποια νίκη. Καταφέραμε και πήραμε την απαιτούμενη ενέργεια στον 4ο κλάδο. Πύρρεια νίκη όμως, διότι οι «αλληλοκλοπές των κλάδων όπως βλέπουμε δεν άλλαξαν καθόλου. Το χειρότερο δε είναι ότι τώρα έχουμε προβλήματα στον 1ο και 2ο κλάδο!!. Τα ποσά των υπερβάσεων τους (23% & 16,3%) συνήθως προξενούν υδραυλικά προβλήματα (Βλ. τελικό σχόλιο στο τέλος του παραδείγματος).

Ο σε εισαγωγικά τίτλος του παραδείγματος αυτού δείχνει την αντίθεσή μας στο πολύ συχνό φαινόμενο της αλλαγής της αντλίας (μάταιης και χωρίς λόγο τις περισσότερες φορές) σε περίπτωση αντιμετώπισης προβλημάτων σε συστήματα θέρμανσης ή ψύξης-θέρμανσης.

Συγκρίνετε το μανομετρικό ύψος της αντλίας (4790 mm Υ.Σ ) με εκείνο της περίπτωσης 3.1 (εξισορροπημένο σύστημα / ισοδύναμοι κλάδοι) οπότε και είναι εύλογη μία απάντηση σε εκείνους που υποστηρίζουν ότι ανεβαίνουν οι απαιτούμενες πιέσεις στα εξισορροπημένα συστήματα .

Β. Μη ισοδύναμοι κλάδοι
Περίπτωση 1.2 Σχήμα 2

Πίνακας 1.2

Επίπεδο	Ζητούμενη παροχή νερού Lit/h	Επιτευχθείσα παροχή νερού Lit/h	Απόκλιση από το ζητούμενο	Απόκλιση από μέσο όρο	Διαφορά από μέγιστη/ελάχιστη απόκλιση
Όροφος 1:	900	1650	83,3%	44,4%	0% / 91,9%
Όροφος 2:	1350	1500	11,1%	8,9%	-35,6% / 56,3%
Όροφος 3:	1800	1700	-5,6%	-5,9%	-50,4% / 41,5%
Όροφος 4:	2700	1900	-29,6%	-47,4	-91,9% / 0%
ΣΥΝΟΛΑ:	6750	6750
Απαιτούμενη διαφορική πίεση δικτύου: 4830 mmΥΣ

Σχόλια:

Η τελευταία στήλη δείχνει το μέγεθος της «καταστροφής». Αν και γίνεται παρακάτω ο τελικός σχολιασμός, εν τούτοις μπορώ να επισημάνω και εδώ ότι το άνοιγμα της ψαλίδας της άδικης κατανομής του νερού κατά 91,9% σε καθημερινή μόνο 10ωρη λειτουργία και για 30 μόνο ημέρες σημαίνει και 750 kWh! ενέργειας αδίκως κατανεμημένης αλλά και 385 kWh! απώλειας από τον 4ο όροφο που θα επιβαρυνθεί το κόστος της και δεν θα έχει ωφεληθεί.

2. Αντεπίστροφο σύστημα.

Α. Ισοδύναμοι κλάδοι
Περίπτωση 2.1.1 Σχήμα 3

Πίνακας 2.1.1

Επίπεδο	Ζητούμενη παροχή νερού Lit/h	Επιτευχθείσα παροχή νερού Lit/h	Απόκλιση από το ζητούμενο	Διαφορά από μέγιστη/ελάχιστη απόκλιση
Όροφος 1:	1350	1345	-0,4%	-0,7% / 0%
Όροφος 2:	1350	1355	0,4%	0% / 0,7%
Όροφος 3:	1350	1355	0,4%	0% / 0,7%
Όροφος 4:	1350	1345	-0,4%	-0,7% / 0%
ΣΥΝΟΛΑ:	5400	5400
Απαιτούμενη διαφορική πίεση δικτύου: 4230 mmΥΣ

Σχόλια:

Το σύστημα πρακτικά θεωρείται πλήρως ισορροπημένο. Εδώ είναι η ευρηματικότητα του συστήματος αυτού που με την ίδια απαίτηση διαφορικής πίεσης όπως η περίπτωση 1.1.1 έρχεται και εξισορροπείται εντελώς από μόνο του. Η διαφορά των 440 mm Υ.Σ σε σχέση με την περίπτωση 1.1.1 οφείλεται στον πρόσθετο σωλήνα Φ42 επιστροφής, από τον 4ο όροφο έως το ισόγειο, τον οποίον απαιτεί το αντεπίστροφο σύστημα όταν είναι κατακόρυφο.

Πάντως το σύστημα επηρεάζεται κάπως από την επιλογή των διατομών του πρωτεύοντος δικτύου. Ενδεικτικά αναφέρουμε ότι σε περίπτωση που μόνο αλλάξει η διατομή του σωλήνα εισαγωγής από τον 1ο έως τον 2ο όροφο καθώς και του «συμμετρικού» του σωλήνα επιστροφής από τον 3ο έως τον 4ο όροφο από Φ42 σε Φ35, επιλογή που θεωρείται μέσα στα επιτρεπόμενα όρια, τότε ο προηγούμενος πίνακας 2.1.1 παίρνει την μορφή 2.1.2

Περίπτωση 2.1.2 Σχήμα 3

Πίνακας 2.1.2

Επίπεδο	Ζητούμενη παροχή νερού Lit/h	Επιτευχθείσα παροχή νερού Lit/h	Απόκλιση από το ζητούμενο	Διαφορά από μέγιστη/ελάχιστη απόκλιση
Όροφος 1:	1350	1385	2,6%	0% / 5,3%
Όροφος 2:	1350	1315	-2,6%	-5,3% / 0%
Όροφος 3:	1350	1315	-2,6%	-5,3% / 0%
Όροφος 4:	1350	1385	2,6%	0% / 5,3%
ΣΥΝΟΛΑ:	5400	5400
Απαιτούμενη διαφορική πίεση δικτύου: 4600 mmΥΣ

Σχόλια:

Οι μικρές αποκλίσεις πού φαίνονται στον παραπάνω πίνακα οφείλονται στο ότι δεν καλύπτεται ακριβώς μία από τις απαιτήσεις του συστήματος αυτού. Η απαίτηση αυτή είναι η δευτερεύουσα προϋπόθεση που γράψαμε προηγουμένως. Δηλαδή ότι το κύριο δίκτυο (στο παράδειγμα μας οι στήλες και σε ένα τμήμα μόνο αυτού) δεν έχει αμελητέες πρακτικά υδραυλικές αντιστάσεις.

Β. Μη ισοδύναμοι κλάδοι
Περίπτωση 2.2 Σχήμα 4

Πίνακας 2.2

Επίπεδο	Ζητούμενη παροχή νερού Lit/h	Επιτευχθείσα παροχή νερού Lit/h	Απόκλιση από το ζητούμενο	Απόκλιση από μέσο όρο	Διαφορά από μέγιστη/ελάχιστη απόκλιση
Όροφος 1:	900	1390	54,4%	29,0%	0% / 61,6%
Όροφος 2:	1350	1400	3,7%	3,0%	-26,1% / 35,6%
Όροφος 3:	1800	1810	0,6%	0,6%	-28,4% / 33,2%
Όροφος 4:	2700	2150	-20,4%	-32,6%	-61,6% / 0%
ΣΥΝΟΛΑ:	6750	6750
Απαιτούμενη διαφορική πίεση δικτύου: 4110 mmΥΣ

Σχόλια:

Αναφέραμε προηγουμένως ότι σε περίπτωση που δεν ισχύει η βασική προϋπόθεση ισοδυναμίας των κλάδων, το αντεπίστροφο σύστημα είναι μία ουτοπία! Ιδού η απόδειξη.

Είναι έντονα παραπλανητικό διότι εφ’ όσον απαιτούμε μικρές παροχές νερού στους πρώτους ορόφους και μεγαλύτερες στους τελευταίους (αν απαιτούσαμε το αντίθετο τότε θα επιλέγαμε και με το δίκιο μας το κλασσικό δίκτυο ακόμη και αρρύθμιστο!), μας δημιουργεί την εντύπωση ότι θα μας ικανοποιήσει την απαίτηση αυτή με μικρό σφάλμα. Μας κάνει βέβαια αρκετή βελτίωση σχετικά με την περίπτωση 1.2, αλλά δεν δικαιολογεί τον ενθουσιασμό μερικών συναδέλφων που το επιλέγουν ακόμη και στις κατακόρυφες στήλες (όπως το παράδειγμα μας) φθάνοντας στο σημείο να «σέρνουν» την τρίτη σωλήνα (από τον 4ο όροφο μέχρι το Ισόγειο).

Το ότι στο παράδειγμα φαίνεται να έχουν μικρές διαφοροποιήσεις οι μεσαίοι κλάδοι, αυτό είναι τυχαίο και δεν σημαίνει ότι συμβαίνει πάντοτε.

Σύστημα εξισορροπημένο.

Α. Ισοδύναμοι κλάδοι
Περίπτωση 3.1 Σχήμα 1

Πίνακας 3.1

Επίπεδο	Ζητούμενη και επιτευχθείσα παροχή νερού Lit/h	Αποκλίσεις και διαφορές	Kv ρυθμιστικών βαλβίδων	Αντιστάσεις ρυθμιστικών βαλβίδων mmΥΣ
Όροφος 1:	1350	0%	3,68	1373
Όροφος 2:	1350	0%	4,36	978
Όροφος 3:	1350	0%	5,74	564
Όροφος 4:	1350	0%	8,70	246
ΣΥΝΟΛΑ:	5400
Απαιτούμενη διαφορική πίεση δικτύου: 4650 mmΥΣ

Σχόλια:

Ανέβηκε η απαιτούμενη διαφορική πίεση περίπου κατά 850 mm Υ.Σ σχετικά με την περίπτωση 1.1.1 που εξετάσθηκε παραπάνω. Πολύ μικρό «μειονέκτημα» σχετικά με το όφελος που αποκομίζουμε από ένα ρυθμισμένο σύστημα. Βέβαια στην περίπτωση αυτή των ισοδυνάμων κλάδων δεν πρέπει να ξεχνάμε ότι υπερέχει το αντεπίστροφο σύστημα (περίπτωση 2.1) το οποίο εξισορροπείται θαυμάσια από μόνο του.

Β. Μη ισοδύναμοι κλάδοι.
Περίπτωση 3.2.1 Σχήμα 2

Πίνακας 3.2.1

Επίπεδο	Ζητούμενη και επιτευχθείσα παροχή νερού Lit/h	Αποκλίσεις και διαφορές	Kv ρυθμιστικών βαλβίδων	Αντιστάσεις ρυθμιστικών βαλβίδων mmΥΣ
Όροφος 1:	900	0%	1,21	5644
Όροφος 2:	1350	0%	2,37	3310
Όροφος 3:	1800	0%	3,55	2623
Όροφος 4:	2700	0%	14,20	369
ΣΥΝΟΛΑ:	6750
Απαιτούμενη διαφορική πίεση δικτύου: 7050 mmΥΣ

Σχόλια:

Πράγματι υπάρχει το αυξημένο απαραίτητο μανομετρικό ύψος αντλίας κατά πως λένε οι προβάλλοντες τα μειονεκτήματα των εξισορροπημένων δικτύων (7050 mm Υ.Σ από 4830 mm Υ.Σ (περίπτωση 1.2) και από 4110 mm Υ.Σ (περίπτωση 2.1)), αλλά αυτό είναι το απαραίτητο μανομετρικό ύψος του δικτύου για να λειτουργήσει σωστά και όχι αυτό που βγαίνει από την γνωστή μέθοδο του απομακρυσμένου βρόγχου η οποία και καταλήγει στις απαράδεκτες καταστάσεις 1.2 και 2.1 που προαναφέραμε. Πρέπει πλέον να γίνει συνείδηση όλων ότι η επιλογή αντλιών βάσει του απομακρυσμένου βρόγχου οδηγεί σε λανθασμένους υπολογισμούς δικτύων.

Περίπτωση 3.2.2 Σχήμα 4
Αντεπίστροφο σύστημα εξισορροπημένο.

Πίνακας 3.2.2

Επίπεδο	Ζητούμενη και επιτευχθείσα παροχή νερού Lit/h	Αποκλίσεις και διαφορές	Kv ρυθμιστικών βαλβίδων	Αντιστάσεις ρυθμιστικών βαλβίδων mmΥΣ
Όροφος 1:	900	0%	1,41	4156
Όροφος 2:	1350	0%	2,72	2513
Όροφος 3:	1800	0%	3,85	2230
Όροφος 4:	2700	0%	14,20	369
ΣΥΝΟΛΑ:	6750
Απαιτούμενη διαφορική πίεση δικτύου: 6360 mmΥΣ

Σχόλια:

Αυτό που θέλω να σχολιάσω εδώ είναι ότι η κατά 700 mm Υ.Σ διαφορά του απαραίτητου μανομετρικού ύψους αντλίας σχετικά με την προηγούμενη περίπτωση, συνεπάγεται μία οικονομία της τάξης των 15 kWh σε 20ωρη καθημερινή λειτουργία και για 30 ημέρες. Ας συγκρίνουμε τώρα το κόστος της ενέργειας αυτής με το κόστος 12 m μήκους εγκατεστημένου σωλήνα διαμέτρου Φ42 που απαιτεί το αντεπίστροφο κατακόρυφο σύστημα και ας υπολογίσουμε σε πόσο χρόνο αποσβένονται 45.000 Δρχ με ρυθμό απόσβεσης 400 Δρχ ανά μήνα. Το αποτέλεσμα του υπολογισμού αυτού είναι προφανές. Απαιτούνται πάνω από 20 χρόνια για να γίνει μία τέτοιου είδους απόσβεση.

Τελικά σχόλια

Ίσως κάποιοι συνάδελφοι αναρωτηθούν γιατί δείχνουμε τόση αυστηρότητα στην κατανομή του νερού μεταξύ των κλάδων. Είναι γεγονός ότι ο λόγος της μεταβολής της απόδοσης ενός θερμαντικού σώματος φυσικής κυκλοφορίας αέρα, προς την μεταβολή της παροχής του νερού είναι περίπου 1:5 (πέφτει στο 1:3,5 στην περίπτωση ψύξης με fan-coils), άρα εάν ένα σώμα υπολογισθεί με 120 Lit/h παροχή νερού και αποδίδει 1.800 Kcal/h, και εάν στην πράξη περάσουν τελικά όχι 120 αλλά 90 Lit/h τότε η πραγματική απόδοση του σώματος πέφτει κατά 90 Kcal/h, πράγμα που με πρώτη ματιά θεωρεί κανείς αμελητέα ποσότητα. Σε ένα διαμέρισμα όμως θερμαντικής απαίτησης 10.000 Kcal/h, μία απόκλιση -25% στην ροή του νερού σημαίνει 5% μείωση της θερμαντικής απόδοσης πού σε 14ωρη καθημερινή λειτουργία σημαίνουν 250 kWh απώλεια ενέργειας ανά μήνα, περίπου όση χρειάζεται στο ίδιο χρονικό διάστημα ένα μέσο νοικοκυριό σε ηλεκτρική ενέργεια!. Με γνώμονα το σχόλιο αυτό, ας ανατρέξουν πάλι οι αναγνώστες στους πίνακες του παραπάνω παραδείγματος και ας προσέξουν ειδικά τις στήλες με τις αποκλίσεις των πραγματικών ροών από τις ζητούμενες.

Εκτός από τις οικονομικές συνέπειες έχουμε και λειτουργικά προβλήματα αυτά που μερικές φορές τα ονομάζουμε και πρακτικά προβλήματα. Είναι πλέον γνωστό σε όλους αυτούς που έχουν την πείρα των κατασκευών των συστημάτων θέρμανσης-κλιματισμού ότι σχεδόν όλα τα προβλήματα στην λειτουργία των συστημάτων αυτών είναι τέτοια που δεν έχουν σχέση με την θερμική μελέτη του συστήματος (φορτία χώρων, επιλογή και υπολογισμός σωμάτων) αλλά με την υδραυλική μελέτη του συστήματος. Στο τεύχος 260/94 (1ο αρθρο) του δελτίου των Μηχανολόγων-Ηλεκτρολόγων και στις σελίδες 54-58 αναφέρονται πολύ αναλυτικά όλα αυτά, εδώ περιοριζόμαστε απλά να τα θυμίσουμε γρήγορα. Είναι προβλήματα θορύβων, συνεχών εξαερισμών των σωμάτων, ασύμμετρων φθορών δικτύου και σωμάτων, χαμηλών θερμοκρασιών επιστροφών, ανομοιόμορφων θερμοκρασιών των σωμάτων μεταξύ πρώτων και τελευταίων στοιχείων κλπ.

Ίσως κάποιοι άλλοι συνάδελφοι αναρωτηθούν γιατί δίνουμε τόση έμφαση στις παροχές του νερού, ενώ θα μπορούσαν αυτές να παίζουν ένα δευτερεύοντα ρόλο στην μελέτη που δεν θα χρειαζόταν να απασχολήσουν τόσο πολύ τον μελετητή. Από εδώ μπορεί να ξεκινήσει μία μεγάλη συζήτηση. Αυτό όμως που θα γραφεί προς στιγμήν είναι ότι η παροχή του νερού, όχι μόνο δεν μπορεί να παίξει δευτερεύοντα ρόλο στο σύστημα, αλλά είναι και ο σημαντικότερος παράγοντας του συστήματος, διότι είναι ο συνδετικός κρίκος μεταξύ του θερμικού μέρους της μελέτης (θερμικά-ψυκτικά φορτία, υπολογισμός σωμάτων), και του υδραυλικού μέρους (υπολογισμός διατομών δικτύου, υπολογισμός αντλιών, υπολογισμός εξισορροπητικών αντιστάσεων κλπ), συνεπώς ο μελετητής, όχι μόνο δεν μπορεί να αδιαφορήσει προς αυτό το μέγεθος αλλά πρέπει να το γνωρίζει και να το ελέγχει αρκετά καλά. Ήδη έχοντας τελειώσει το θερμικό μέρος της μελέτης, οι παροχές του νερού είναι πλέον δεδομένες και αυτό που πρέπει να κάνει στην συνέχεια είναι ένα δίκτυο, που να προσαρμόζεται πλήρως σε αυτές.

Όπως θα προσέξατε στα σχήματα: "κατακόρυφο 1" και "κατακόρυφο 2" η εξισορρόπηση του δικτύου έγινε με μία κεντρική βαλβίδα στην επιστροφή, μεταξύ συλλεκτών και στηλών. Με αυτόν τον τρόπο εξασφαλίζουμε την σωστή κατανομή νερού μεταξύ των διαμερισμάτων του κτηρίου που είναι ουσιαστικότερο από την αυστηρή κατανομή του νερού μεταξύ των χώρων του ίδιου διαμερίσματος. Αυτή είναι μία εναλλακτική μέθοδος εξισορρόπησης και πολλές φορές προσεγγίζει αρκετά ικανοποιητικά την κλασσική εξισορρόπηση (εξισορρόπηση βρόγχων). Η επιτυχία της εξαρτάται από την συμμετρία των φορτίων και των υδραυλικών κυκλωμάτων. Έχει λειτουργήσει με επιτυχία στην πράξη τόσο στα συστήματα ψύξης-θέρμανσης όσο και στα μονοσωλήνια συστήματα.

Επίλογος

Από όλα όσα γράφηκαν προηγούμενα βγαίνει το συμπέρασμα ότι η μελέτη ενός συστήματος πλέον, πρέπει να συμπεριλαμβάνει μία ουσιαστική υδραυλική ανάλυση του δικτύου. Βέβαια όλοι γνωρίζουμε ότι η υδραυλική ανάλυση είναι πολύ πιο σύνθετη από την θερμική ανάλυση (θερμικά κυκλώματα μονοσωληνίου συστήματος κλπ) και ακόμη πιο πολύ από τις θερμικές απώλειες, ακόμη γνωρίζουμε ότι ο χειροκίνητος υπολογισμός (από πλευράς όγκου εργασίας) είναι σχεδόν αδύνατος, αλλά όλοι γνωρίζουμε επίσης ότι πλέον, κάθε μηχανικός σήμερα, διαθέτει έναν προσωπικό υπολογιστή όπου χρησιμοποιώντας τον φιλοδοξεί να παρουσιάσει μία ολοκληρωμένη εργασία (και όχι μόνο από πλευράς εμφάνισης) με τις σημερινές τεχνικές και όχι με εκείνες της περασμένης δεκαετίας.

Τέλος θέλουμε να σημειώσουμε ότι επειδή η συγκεκριμένη ανάλυση όπως όλοι γνωρίζουν δεν είναι απλή και δεν γίνεται με απλούς υπολογισμούς, χρησιμοποιήθηκε εξειδικευμένο πρόγραμμα του Γ. Βαρβαγιάννη που η ανάλυσή του έχει ενσωματωθεί στα μηχανολογικά πακέτα της Ti-Soft δηλαδή τα πακέτα Pipes-cad, Thermo-cad.

Στείλτε μας την γνώμη σας γι' αυτή την σελίδα (Επιλέξτε και πατήστε: Αποστολή)
Χρήσιμη σελίδα...	Δεν συμφωνώ ή μου είναι αδιάφορη
Ακόμη, αν θέλετε να μας στείλετε κάποιο κείμενο, μπορείτε να το γράψετε στο παρακάτω edit-box και να πατήσετε Αποστολή. Αν θέλετε απάντηση πρέπει στο σχόλιο να συμπεριλάβετε και το e-mail σας διότι δεν μπορώ να το δω από το μήνυμά σας και μόνο.